Math
Calculus - The Derivatives

---

Calculus is used to measure a quantity that is continuously changing. For example the distance a moving car is from its starting position is constantly changing. To calculate the average speed, we simply divide the distance gone by the time taken. Let f(x) be the distance traveled in time x, then the average speed during the interval from x to x + h is

 

 

However to find the instantaneous speed (when h = 0) we have to take a limit as this ratio as the time interval (h) approaches 0. The function that results when we take a limit measures the instantaneous speed of the car (the rate at which the distance is changing with respect to time). We call this function a first derivative. The second derivative of distance is acceleration.

 

 

There are several shortcuts to this formula. Here is a partial list:

 

1.

2.

3.

4.

5.

6.

7.

 

8.  Product rule 

 

For example:

 

9.  Quotient rule

 

For example:

 

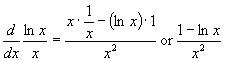
10.  Chain rule:

 

For example:

 

The derivative f’(x) is the slope of the graph of the function f. It is also the instantaneous rate at which f is changing with respect to x. A common question is what is the maximum (minimum) value of the function f? Both of these values exist where the derivative (slope) is equal to zero. And so we solve the equation f’(x) = 0. Occasionally these extreme values occur where the derivative is undefined.