Math
Exercise 11
1. Given the following histograms of data set A and data set B:
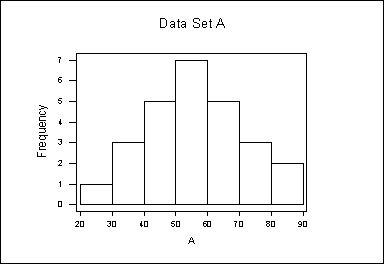
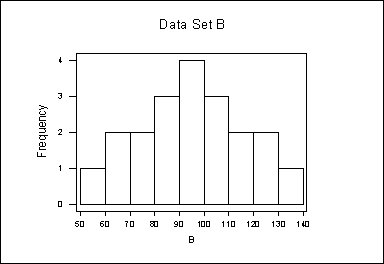
i) Which data set has a larger mean?
(a) |
A |
(b) |
B |
(c) |
both have approximately the same mean. |
||
ii) Which data set has the larger standard deviation?
(a) |
A |
(b) |
B |
(c) |
both have approximately the same standard deviation. |
||
iii) Which data set has the larger range?
(a) |
A |
(b) |
B |
(c) |
both have approximately the same range |
||
i) (b) B ii) (b) B iii) (b) B
See graph below.
i) b) B has a larger mean
ii) b) B has more spread around the mean
iii) b) B has the largest range (distance between highest and lowest measurement)
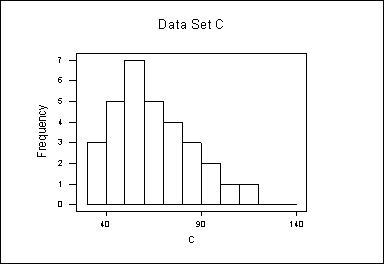
2.Given the data graphed below, is the mean or the median larger?
(a) |
mean |
(b) |
median |
(c) |
both are about the same |
||
(a) mean
The mean is more susceptible to skewed distributions and outliers.
3. The mean, median and mode are measures of the _______________ of the data set.
(a) |
centre |
(b) |
range |
(c) |
skew |
(d) |
spread |
(b) centre
Definition
4. Variance is a measure of the ____________ of a data set.
(a) |
centre |
(b) |
range |
(c) |
skew |
(d) |
spread |
(d) spread
Definition
5. An outlier is a score that is much larger or much smaller than the other scores in a data set. Which statistic is most susceptible to a single outlier?
(a) |
mean |
(b) |
median |
(c) |
mid quartile range |
(d) |
mode |
(a) mean
See 2. above.
6. A golfer has the following scores: 74, 69, 70, 70, 73, 70, 68, 71, 71, 74. Calculate the following statistics. In each case choose the option that is closest to the correct answer:
i) mean
(a) |
2 | (b) |
4 | (c) |
68 | (d) |
70 |
(e) |
70.5 | (f) |
71 | (g) |
74 |
(f) 71
See the formula 710/10
ii) median
(a) |
2 | (b) |
4 | (c) |
68 | (d) |
70 |
(e) |
70.5 | (f) |
71 | (g) |
74 |
(e) 70.5
See the formula (70+71)/2
iii) mode
(a) |
2 | (b) |
4 | (c) |
68 | (d) |
70 |
(e) |
70.5 | (f) |
71 | (g) |
74 |
(d) 70
The measurement of 70 occurred the most.
iv) standard deviation
(a) |
2 | (b) |
4 | (c) |
68 | (d) |
70 |
(e) |
70.5 | (f) |
71 | (g) |
74 |
(a) 2
1) Take the difference between each measurement and the mean
2) square the outcome
3) add up
4) divide by n-1
5) take the square root
v) variance
(a) |
2 | (b) |
4 | (c) |
68 | (d) |
70 |
(e) |
70.5 | (f) |
71 | (g) |
74 |
(b) 4
Square the standard deviation
7. Consider a deck of playing cards: ace through king in suits of hearts, diamonds (both red) spades and clubs (both black):
i) Choose one card at random. What is the probability that it is a four?
(a) |
0.02 |
(b) |
0.08 |
(c) |
0.25 |
(d) |
0.5 |
(b) 0.08
13 cards in each 4 suits, so we have 4 fours in 52 cards
ii) Choose one card at random. What is the probability that it is a spade?
(a) |
0.02 |
(b) |
0.08 |
(c) |
0.25 |
(d) |
0.5 |
(c) 0.25
4 suits
iii) Choose one card at random. What is the probability that it is a face card (a jack, a queen or a king)?
(a) |
0.08 |
(b) |
0.23 |
(c) |
0.25 |
(d) |
0.5 |
(b) 0.23
Each suit (13 cards) has 3 face cards. 3/13 = 0.2307...
8. Select two cards at random from the deck. Do not replace the first card before selecting the second card. What is the probability that both cards are hearts?
(a) |
0.059 |
(b) |
0.063 |
(c) |
0.25 |
(d) |
0.3 |
(a) 0.059
1) First draw: one out of four = 25%
2) 51 cards left, 12 hearts, so second draw is 12/51 chance
3) total chance is 0.25 x 12/51 = 0.059