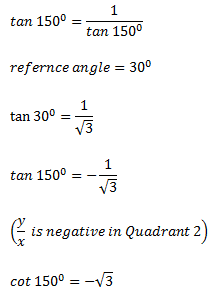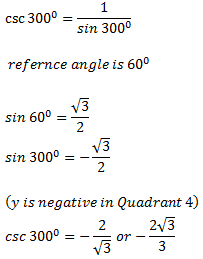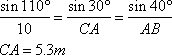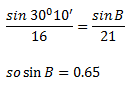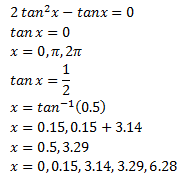return to standard view
Print Questions & Answers Print Questions
Table of Contents | Workbook: Lessons & Exercises

Math
Exercise 9

 

Choose the best answer.


Question 1:

Give the exact value of sin 120o. 

(a)

(b)

(c)

(d)

 

(a)

 


Question 2:

Give the exact value of cot 150o.

(a)

(b)

(c)

(d)

 

(a)

 


Question 3:

Give the exact value of cos 225o 

(a)

(b)

(c)

(d)

 

(a)

 

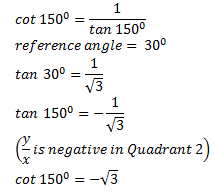Question 4:

Give the exact value of csc 300o

(a)

(b)

 2/3

(c)

(d)

 2

 

(a)

 

 


Question 5:

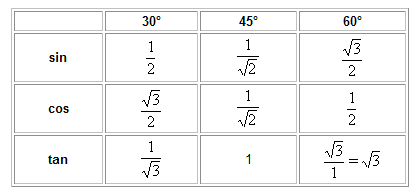
Give the exact value of      (radians) 

(a)

(b)

(c)

(d)

 

(c)

 

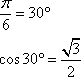See table

 

Question 6:

Give the exact value of     (radians) 

(a)

(b)

(c)

(d)

 

(c)

 


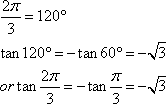Question 7:

If the angle of elevation of the sun is 36o, how long a shadow (in feet) will a 6 foot person cast on level ground? 

(a)

 3

(b)

 4

(c)

 8

(d)

 10

 

(c)
 8

 



Question 8:

Two students are asked to find the height and the location of a balloon. They select two points, A and B, on level ground. From A, the angle of elevation of the balloon is 35o and from B, the angle of elevation of the balloon is 67o. If the distance between A and B is 80m and the balloon is between A and B:

i) Calculate the height of the balloon. Choose the option that is closest to the correct answer. 

 

(a)

 43 m

(b)

 50 m

(c)

 60 m

(d)

 75 m

 

(a)
 43 m

 

We know that all angles of a triangle together will be 180 degrees, so the third angle is 78 degrees.

Make a sketch from the situation, looking at it from the sight.

Now look at the law of sines and the sketch in your book.
Assume that A = person A, B = balloon and C = person B.

Now we can write:

sin 35o
=
sin 78o
=
sin 67o
   a
   80
   c

Here c is the distance from person A to balloon = 81.8 sin 67o = 75.3 m

Height of the balloon: sin 35o = height/75.3 , so the height is 43 m.

 

 

ii) What is the horizontal distance between A and the balloon? Choose the option that is closest to the correct answer.  

 

(a)

 40 m

(b)

 50 m

(c)

 62 m

(d)

 75 m

 

(c)
 62 m

 

Horizontal distance is a point on line AB.

cos 35o = distance/75.3, so the distance is 62 meters.

 

Question 9:

Evaluate

(a)

 60o

(b)

(c)

(d)

 45o

 

(d)
 45o

 

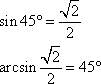
see table

 

Question 10:

Evaluate

(a)

(b)

(c)

 45o

(d)

 120o

 

(a)

 


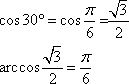Question 11:

Evaluate  Arc tan 1 (or tan-1 1) 

(a)

(b)

(c)

(d)

 

(c)

 


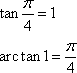Question 12:

In triangle ABC, BC = 10 m, , .

 

i) Find

(a)

 30o

(b)

 40o

(c)

 90o

(d)

 110o

 

(d)
 110o

 

 Angles of a triangle sum to 180°.

 

ii) Find CA

(a)

 2

(b)

 5

(c)

 7

(d)

 18

 

(b)
 5

 

Use the law of sines:

 

Question 13:

A surveyor stands on a cliff that is 25 feet above the water in the river below. The angle of depression to the waters edge on the opposite bank is 12o35'. How wide (in feet) is the river at this point? 

(a)

 5

(b)

 50

(c)

 110

(d)

 113

 

(d)
 113

 

Draw the situation. The cliff edge equals the opposite. The adjacent site is the width of the river. Use the tangent of the angle of depression.


Question 14:

In triangle ABC, = 100o, BC = 15 m, AC = 20 m. Find AB. 

(a)

 22

(b)

 30

(c)

 500

(d)

 730

 

(a)
 22

 

Use the law of cosines: c2 = (15)2 + (20)2 - 2 (15) (20) (cos 100°)

c2 = 521,
so c = 22.8 m

 


Question 15:

From an airport at noon one airplane flies NE at 300 mph, another due south at 400 mph. How far apart are they at 2 pm? 

(a)

 566

(b)

 1273

(c)

 1385

(d)

 2125

 

(a)
 566

 

 Use the law of cosines:
b2 = (800)2 + (600)2 -2 (600) (800) cos 135° = 321178
So the planes are 566 miles apart.



Question 16:

In triangle ABC, , ,

(a)

 40o

(b)

 40o and 140o

(c)

 22o

(d)

 No such triangle exists.

 

(b)
 40o and 140o

 

 


Question 17:

The support for a solar panel is triangular in cross section. The sides of the triangle have lengths 0.4m, 1.4m and 1.4m. What is the angle between the two sides that are 1.4 m long? 

(a)

 10o

(b)

 16o

(c)

 50o

(d)

 80o

 

(b)
 16o

 

Use the law of cosines:
(0.4)2 = (1.4)2 + (1.4)2 - 2 (1.4) (1.4) cos x
so, cos x = 0.959, so x = 16.4 m

 

Question 18:

At a point near a tree you find that the angle of elevation of the top of a tree is  32.5o. If you move 25 feet closer to the tree, the angle of elevation becomes 42.3o.  If the ground is level, what is the height of the tree (in feet)? 

(a)

 25

(b)

 45

(c)

 75

(d)

 100

 

(b)
 45

 

Draw the picture. Define the distance between the tree and the second position as d.

You get two equations:
tan (32.5o) = height/(d+25)
tan (42.3o) = height/d

Substitute one in the other and get:
0.6 d + 15 = 0.9 d, so 0.3 d = 15, so d = 50
so the tree height is 0.9d = 45 feet


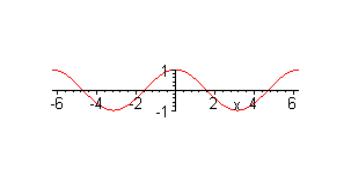
Question 19:

Which equation describes the graph below? 

(a)

 y = sin x 

(b)

 y = cos x

(c)

 y = tan x

(d)

 y = cot x

 

(b)
 y = cos x

 

 Since the curve starts at 1, it is a cos x.


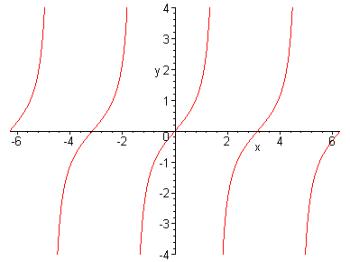
Question 20:

Which equation describes the graph below? 

(a)

 y = sin x 

(b)

 y = cos x

(c)

 y = tan x

(d)

 y = sec x

 

(c)
 y = tan x

 

 Typical shape of the tan x!


Question 21:

Which equation describes the graph below? 

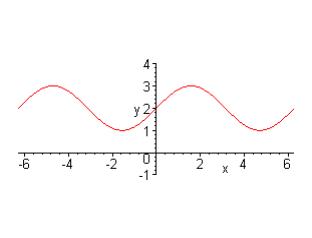
(a)

 y = 2 + sin x  

(b)

 y = 2 – sin x

(c)

 y = sin 2x

(d)

 y = sin (x + 2)

 

(a)
 y = 2 + sin x  

 

 Where 0 should be, we read 2, so we ad 2 to every y value of the original curve. y = sin x is shifted up two units, or has a vertical translation of 2 units.

 


Question 22:

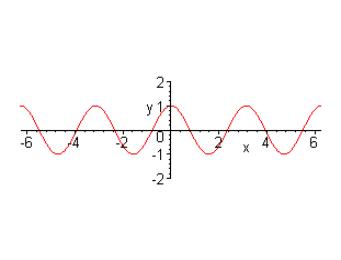
(a)

 y = cos (x + 2)  

(b)

 y = cos (x – 2)

(c)

 y = cos 2x 

(d)

 y = cos ½x

 

(c)
 y = cos 2x 

 

 The wave moves twice as fast, with only half of the x-axis needed per wave length.

y = cos x is shrunk by a factor of two, or has a horizontal stretch of 1/2.

 


Question 23:

Find all values of x in [0o, 360o] that satisfy the equation sin 3x = 0.34. 

(a)

 25o

(b)

 7o, 55o, 127o, 174o, 247o, 294o

(c)

 20o, 160o

(d)

 5o

 

(b)
 7o, 55o, 127o, 174o, 247o, 294o

 

Since the sine curve repeats itself every 360o, the solution is:
3x = 19.9o + 360o k, so x = 7o + 120o k
3x = sin-1 (0.34) = 19.9o and 160.1o

3x = 19.9o + 360o k and 3x = 160.1o + 360o k

x = 7o + 120o k and x = 54.4o + 120o k

x = 7o, 127o, 247o, 54.4o, 174.4o, 294.4o

6 possible answers



Question 24:

Find all values of x in [0o, 180o] that satisfy the equation sec 2x = 4.5. 

(a)

 35o
(b)
 36o, 144o

(c)

 60o

(d)

 60o, 120o

 

(b)
 36o, 144o

 

sec 2x = 4.5, so 1/cos 2x = 4.5, so cos 2x = 1/ 4.5
so 2x = cos-1(1/ 4.5) = 77o and -77o.

So the answers will be:
2x = 77o + 180o
and
2x = -77o + 180o.

The answers will be therefore 36o and 144o.


Question 25:

Find all real numbers in
 
that satisfy the equation  2tan2 x = tan x.  Use radian mode on your calculator. 

(a)

 0.5, 3.6 

(b)

 0.5, 2.6 

(c)

 0.5, 5.8 

(d)

 0, 3.14, 6.28, 0.15, 3.29

 

(d)

 

 

Back Next