Math
Vectors

---

Consider a point P at (x, y).  The vector , represented by an arrow extending from the origin to P is represented as (x , y).  The magnitude of the vector is the length of the arrow and the direction is the angle it makes with one of the axis. In 3 dimensions we add a third coordinate and get a point P(x, y, z) and the corresponding vector .

 

If we have vectors and the sum defined to be (3 + 1, 2 + 4) or (4, 6).  Recall the parallelogram law.

 

 

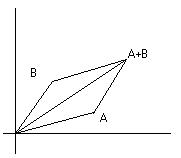
In general if and then

 

or in three dimensions

 

If the vector then the vector (same magnitude, opposite direction). We can therefore define the difference of vectors.

 

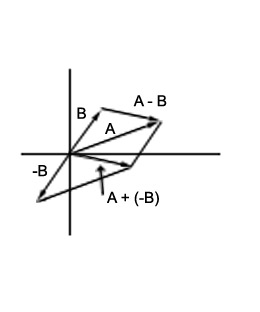
If vector A is and B is then

 

For example let and . Then or

 

In three dimensions we have: If and then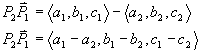

 

The magnitude of a vector is the length of the arrow. In two dimensions the magnitude of . In three dimensions the magnitude of .

 

Frequently it is useful to use unit vectors or vectors of magnitude 1. The basic unit vectors in three dimensions are i = (1, 0, 0), j = (0, 1, 0) and k = (0, 0, 1).  Using this notation the vector (a, b, c) can be also written ai + bj + ck.