Math
Trigonometry and Geometry
Triangle definitions:
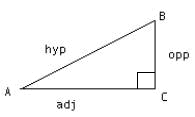
Given the right triangle above with the length of the sides labelled as adjacent, opposite, and hypotenuse.
We then have the following definitions:
|
|
Unit Circle Definition:
Another definition for the trigonometric functions makes use of a unit circle (a circle centred at the origin with radius one). Think of the zero of a number line being placed at the point (1,0), the point where the unit circle crosses the positive x-axis. The positive side of the number line is wrapped counter-clockwise about the circle. The negative side of the number line is wrapped clockwise around the circle. The numbers on the number line now have a location (x, y) on the plane. See diagram.
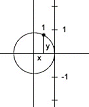
As an example, the number 1 on this circular number line is a point, which has a x-coordinate and a y-coordinate. The sine of 1 is equal to the y-coordinate. The cosine of 1 is the x-coordinate. In general, if t is any number of this number line:
sin t = y |
cos t = x |
where t is the point (x,y). |
These definitions are consistent with the triangle definitions given above for angles of less than 90o in size and they neatly handle angles larger than 90o. A second advantage is that the trigonometric functions are no longer based just on angles. The variable t represents a number with no assumed units. We can now use these functions to model any periodically changing value.
The trigonometric functions take an angle and convert it into a ratio of lengths of sides (using the triangle definition). The arc or inverse functions do the reverse. They take a ratio and return an angle.
If sin t = y |
then t = arcsin y |
or t = sin-1 y |
Strictly speaking arcsin y is not a function. There are an infinite number of angles that would return the ratio y using the sine function. Do not confuse these relations with the reciprocal functions csc t, sec t and cot t.
Following are two laws that are very useful when solving for parts of a triangle.
Given the triangle below:
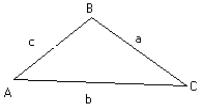
Law of Sines:
![]()
Law of Cosines:
a2 = b2 + c2 – 2bc cos A
b2 = a2 + c2 – 2ac cos B
c2 = a2 + b2 – 2ab cos C