Math
Calculus - The Integral

---

Integration is the inverse operation of differentiation. If we have a function that measures distance with time the derivative will give us the speed. If we have a function that gives us speed then integration will give us a distance function.

 

Note that it will not give us the distance function. For example if f (x) = x² - 4 then f ' (x) = 2x. However when we integrate 2x we get x² + C.  C is the constant of integration. If we want to recover the 4 in the original equation we need more information, a point on the graph for instance.

 

For example, solve for y if 

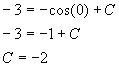
And so the solution is y(x) = -cos x - 2

 

 

Some of the formulas for integration are:

1. provided

2.

3.

4.

5.

6.

7.

The geometrical interpretation of the integral is the area under the curve over some interval on the x-axis. then represents the area under the function between . This definite integral can be solve using the following formula:

 

where F is the anti-derivative of f.

For example:

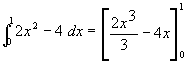
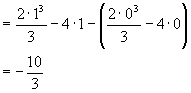
Occasionally when integrating, it is useful to simplify the problem by making a substitution. For example, consider the integral
. If we let u = 3x and so the problem becomes . This integral can be easily solved using the formulas above. Once we have the anti-derivative we can do another substitution to replace the x.