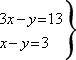Math
Exercise 7
Choose the best answer. Solve the following systems:
Question 1:
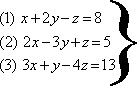
(a) |
x = 5 | (b) |
y = 1 |
(c) |
z = 2 | (d) |
y = 5 |
(a) |
x = 5 |
|
Solution is x=5, y=2, z=1 OR (5,2,1) We’ll use the Gaussian elimination here (which is all about adding and subtracting equations): Add equations (1) and (2) to eliminate z: 3x-y=13 Add 4 times equations (2) and (3) to eliminate z again: 11x-11y=33 OR x-y=3 Now solve system by substitution:
Substitute x and y into an original equation to find z=1. |
Question 2:
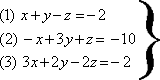
(a) |
x = -3 | (b) |
y = -3 |
(c) |
z = 2 | (d) |
z = -2 |
(b) |
y = -3 |
|
Add equations (1) and (2) to eliminate x and z: 4y=-12 y=-3 Substitute y into equations (1) and (3) to solve simpler system and find x=2 and z=1 |
Question 3:
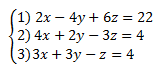
(a) |
x = 2 | (b) |
y = -1 |
(c) |
z = 3 | (d) |
there is no solution |
(b) |
y = -1 |
|
Keep equation 3, eliminate z in eq. 2 and eq. 1 equation 1 + 2(equation 2) = new equation 2 20x + 14 y = 46 Now find the values by filling in your answers:
|
Question 4:
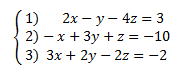
(a) |
x = 1 | (b) |
y = 2 |
(c) |
z = 1 | (d) |
there is no solution |
(c) |
z = 1 |
|
Use equation (2) to eliminate x 5y – 2z = -17 put z from eq 3 in eq 1: y = -3 |
Question 5:
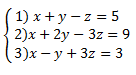
(a) |
x = 1 | (b) |
y = -4 |
(c) |
z = -1/2 | (d) |
there is no solution |
(d) |
there is no solution |
|
Keep equation 1, subtract eq.1 from both eq. 2 and eq. 3 x + y – z = 5 Now do this: 2 (eq. 2) + eq. 3 = new equation 3 |
Question 6:
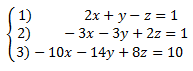
(a) |
x = 2 |
(b) |
y = x - 3 |
(c) |
z = 4 – 3x |
(d) |
there is no solution |
(b) |
y = x - 3 where x is any real number |
|
Use eq 1 to eliminate z in eq 2 and 3: |
Question 7:
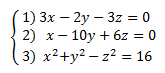
(a) |
x = ±4 | (b) |
y = ±8 |
(c) |
z = ±3 | (d) |
there is no solution |
(c) |
z = ±3 |
|
Take y out of equation 1 and x out of equation 2: put x from eq 2 in eq 1 and y from eq 1 in eq 2 Now put x and y in eq 3: |