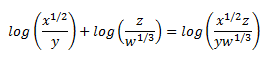Math
Exercise 6
Choose the best answer.
Question 1:
What is the value of log162 ?
(a) |
⅛ | (b) |
¼ |
(c) |
½ | (d) |
8 |
(b) |
¼ |
|
Use Rule 7 and choose a log that gives obvious answers with 2 and 16: |
Question 2:
What is the value of ln e-5?
(a) |
e-5 | (b) |
10-5 |
(c) |
-5 | (d) |
10e |
(c) |
-5 |
|
Use Rule 5. |
Question 3:
What is the value of log 1?
(a) |
0 | (b) |
|
(c) |
1 | (d) |
10 |
(a) |
0 |
|
Use Rule 4. |
Question 4:
What is the value of log2(log216)?
(a) |
2 | (b) |
4 |
(c) |
8 | (d) |
16 |
(a) |
2 |
|
log2 16 = 4, so log2 4 = 2 |
Question 5:
What is the value of log71?
(a) |
(b) |
0 | |
(c) |
(d) |
1 |
(b) |
0 |
|
See Rule 4. |
Question 6:
Solve for x: log3 x = ½
(a) |
0.33 | (b) |
1.5 |
(c) |
1.7 | (d) |
6 |
(c) |
1.7 |
|
Use the definition: the solution is 31/2 which is |
Question 7:
Solve for x: logx81 = 4
(a) |
3 | (b) |
4 |
(c) |
20 | (d) |
324 |
(a) |
3 |
|
Which means according to the definition of logarithm that x4 = 81, so x = 3 |
Question 8:
Solve for x: ![]()
(a) |
0.03 | (b) |
0.22 |
(c) |
0.67 | (d) |
0.89 |
(c) |
0.67 |
|
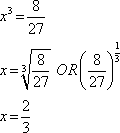 |
Question 9:
Solve for x: x ln 3 = ln 7
(a) |
0.85 | (b) |
1.8 |
(c) |
2.1 | (d) |
3.0 |
(b) |
1.8 |
|
x= ln7/ln3 = 1.7 |
Question 10:
Solve for x: 32x = 4x+1
(a) |
0.39 | (b) |
1.0 |
(c) |
1.71 | (d) |
2.1 |
(c) |
1.71 |
|
Take the natural logarithm of both sides and convert to 2x ln3 = (x+1) ln4 |
Question 11:
The amount of carbon 14 present after t years is given by A(t) = A0ekt where ![]()
i) Find the half-life of carbon 14 in years
(a) |
1400 | (b) |
2800 |
(c) |
5600 | (d) |
11,200 |
(c) |
5600 |
| To find the half-time: Use A(t) = ½ and A0 =1 |
ii) Charcoal from an ancient fire pit on Java had ¼ the amount of carbon 14 found in a living sample of the same size. Estimate the age of the charcoal in years.
(a) |
2800 | (b) |
5600 |
(c) |
11,200 | (d) |
22,400 |
(c) |
11,200 |
|
Use A(t) = ¼ and A0 = 1 |
Question 12:
Solve for x: (x – 1) log 5 = (x – 2) log 9
(a) |
0.73 | (b) |
4.74 |
(c) |
5.53 | (d) |
6.48 |
(b) |
4.74 |
|
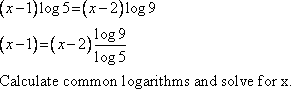 |
Question 13:
Write the following expression as a sum or difference of multiples of logarithms using the properties of logarithms.
![]()
(a) |
½(ln x + ln 4) | (b) |
½(ln x – ln 4) |
(c) |
2(ln x – ln 4) | (d) |
2 (ln x + ln 4) |
(b) |
½(ln x – ln 4) |
|
½ ln (x/4) = ½ (ln x – ln 4) |
Question 14:
Write the following expression as a sum or difference of multiples of logarithms using the properties of logarithms.
![]()
(a) |
3(ln x – ln (x + 4)) | (b) |
3 ln x – ln x – ln 4 |
(c) |
3 ln x – ln x + ln 4 | (d) |
3 ln x – ln (x + 4) |
(d) |
3 ln x – ln (x + 4) |
|
ln x3 – ln (x+4) = 3 lnx – ln (x+4) |
Question 15:
Rewrite the expression as a single logarithm: ½ log x – log y + log z – 1/3 log w
(a) |
(b) |
||
(c) |
(d) |
(a) |
|
|
log x1/2 – log y + log z – log w1/3 =
|
Question 16:
Biologists studying salmon have found that the oxygen consumption of yearly salmon increases exponentially with the speed of swimming according to the function:
f(x) = 100e0.6x where x is speed in feet per second.
i) Find the oxygen consumption when the fish are still.
(a) |
100 | (b) |
150 |
(c) |
182 | (d) |
272 |
(a) |
100 |
| fish are still, (so x=0),
so f(0) = 100 e0 = 100 |
ii) Find the oxygen consumption when the fish in the above question are swimming at 2 feet per second.
(a) |
182 | (b) |
272 |
(c) |
332 | (d) |
1585 |
(c) |
332 |
|
x = 2 feet/second,
so f(2) = 100 e0.6(2) = 332 |
Question 17:
The pH of a solution is defined by pH = - log[H+] where H+ measures the concentration of hydrogen ions in the solution. Acid rain can have a pH of 4. The pH of pure water is 7. How much greater is the concentration of hydrogen ions in such acid rains than in pure water.
(a) |
10 times | (b) |
100 times |
(c) |
1000 times | (d) |
10,000 times |
(c) |
1000 times |
|
4 = -log [H+], so [H+] = 10-4 7 = -log [H+], so [H+] = 10-7 So 1000 times greater (note the minus!). |
Question 18:
A typical mixture of laundry soap and water for laundry has a pH of about 11, while black coffee has a pH of about 5. How much greater is the concentration of hydrogen ions in black coffee than in laundry water?
(a) |
1,000 times | (b) |
10,000 times |
(c) |
100,000 times | (d) |
1,000,000 times |
(d) |
1,000,000 times |
|
10-5compared to 10-11 so 1,000,000 times greater. |