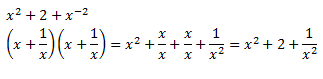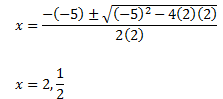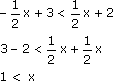Math
Exercise 2
Choose the best answer.
Question 1:
Expand and simplify
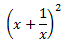
(b) |
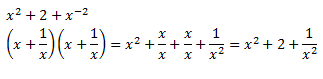 |
Question 2:
Expand and simplify
(2a – 3b)2
(a) |
4a2 – 6ab + 9b2 |
(b) |
4a2 – 6ab – 9b2 |
(c) |
4a2 – 12ab + 9b2 |
(d) |
4a2 – 12ab – 9b2 |
(c) |
4a2 – 12ab + 9b2 |
|
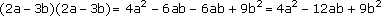 |
Question 3:
Expand and simplify
(3x – 2y)(9x2 + 6xy + 4y2)
(a) |
27x3 – 8y3 |
(b) |
27x3 + 6xy – 8y3 |
(c) |
27x3 + 36x2y + 24xy2 + 8y3 |
(d) |
27x3 – 36x2y + 24xy2 – 8y3 |
(a) |
27x3 – 8y3 |
|
3x·9x2 + 3x·6xy + 3x·4y2 - 2y·9x2 - 2y·6xy – 2y·4y2
= 27x3+18x2y + 12xy2-18x2y
- 12xy2 - 8y3
= 27x3 - 8y3 |
Question 4:
Expand and simplify
2(3a – 2b)2 – (2a + 5b)2
(a) |
14a2 – 4ab + 23b2 |
(b) |
14a2 – 33b2 |
(c) |
14a2 + 21b2 |
(d) |
14a2 – 44ab – 17b2 |
(d) |
14a2 – 44ab – 17b2 |
|
2(3ab-2b) (3ab-2b) – (2ab+5b) (2ab+5b)
= 2(9a2 -6ab-6ab+4b2) – (4a2+10ab+10ab+25b2)
=18a2-24ab+8b2-4a2-20ab-25b2
=14a2-44ab-17b2
|
Question 5:
Simplify
3xy2(-2xy-1)3
(a) |
-24x4y-1 |
(b) |
24x4y-1 |
(c) |
-6x4y5 |
(d) |
6x4y5 |
(a) |
-24x4y-1 |
|
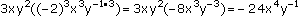 |
Factor completely:
Question 6:
4x – 8y
(a) |
2(2x – 6y) |
(b) |
4xy(1 – 2y) |
(c) |
4x(1 – 2y) |
(d) |
4(x – 2y) |
(d) |
4(x – 2y) |
|
Common factor is 4. |
Question 7:
a2 – 9b2
(a) |
(a – b)(a + 9b) |
(b) |
(a – 9b)(a + 9b) |
(c) |
(a – 3b)(a + 3b) |
(d) |
(a – 3b)2 |
(c) |
(a – 3b)(a + 3b) |
|
a² -3ab + 3ab – 9b² = (a-3b)(a+3b)
Remember this one! You will see this more often. Differences of
squares x2 + y2 = (x-y)(x+y) |
Question 8:
8x2 + 18
(a) |
2(4x2 + 9) |
(b) |
2(2x + 3)2 |
(c) |
2(2x – 3)2 |
(d) |
(8x + 9)(x + 2) |
(a) |
2(4x2 + 9) |
|
Common factor of 2 |
Question 9:
15x2 (x – 1)2 + 10x (x-1)3
(a) |
5x(x – 1)(3 – 2x) |
(b) |
5x(x – 1)2(5x – 2) |
(c) |
5x2(x – 1)2(2x + 1) |
(d) |
5x2(x – 1)(2x + 1) |
(b) |
5x(x – 1)2(5x – 2) |
|
Take 5x(x-1)2 outside the brackets and write the equation as
5x(x-1)2 (3x +2(x-1)).
Common factor of 5x(x-1)2.
5x(x-1)2(3x+2(x-1)) = 5x(x-1)2(5x - 2) |
Question 10:
2x2 + 7xy – 15y2
(a) |
(2x + 3y)(x + 5y) |
(b) |
(2x – 5y)(x + 3y) |
(c) |
(2x – 3y)(x + 5y) |
(d) |
(2x – 3y)(x – 5y) |
(c) |
(2x – 3y)(x + 5y) |
|
Factor by decomposition:
Two factors which multiply to -30 and add to 7 are 10 and -3:
2x2 + 10xy - 3xy - 15y2 =
2x (x + 5y) - 3y (x + 5y) =
(2x – 3y)(x + 5y) |
Question 11:
xy + x – y – 1
(a) |
(x + 1)(y + 1) |
(b) |
(x + 1)(y – 1) |
(c) |
(x – 1)(y – 1) |
(d) |
(x – 1)(y + 1) |
(d) |
(x – 1)(y + 1) |
|
To get -1, you need a “+1” in one term and a “-1” in the other term.
Only answer d can give you a “-y”.
Factor by grouping
xy + x - y - 1 = x (y + 1) -1 (y + 1) = (x - 1)(y + 1) |
Question 12:
12a4 + 19a2 – 18
(a) |
(3a2 – 2)(4a2 + 9) |
(b) |
(6a2 – 2)(2a2 + 9) |
(c) |
(6a2 – 9)(2a2 + 2) |
(d) |
(12a2 + 6)(a2 – 3) |
(a) |
(3a2 – 2)(4a2 + 9) |
|
All terms are the same, except for the “19 a2”. You need a combination of the two terms giving you the “a2”.
Factor by decomposition
Two factors which multiply to -216 and add to 19 are 27 and -8
12a4+27a2-8a2-18 = 3a2(4a2+9)-2(4a2+9)
= (3a2-2)(4a2+9) |
Question 13:
2y4 – 32x4
(a) |
2(y – 2x)(y + 2x)3 |
(b) |
2(y – 2x)(y + 2x)(y2 + 4x2) |
(c) |
2(y – 2x)4 |
(d) |
2(y2 – 4x2)2 |
(b) |
2(y – 2x)(y + 2x)(y2 + 4x2) |
|
There are more ways to solve this. This is one of them: Both answer c and d give you a “+” in the x2-term and can be discarded. Now check to eliminate all terms other than x4 and y4.
Now look at answer b:
(y-2x)(y+2x) = y2 - 4x2, thus giving 2 (y2 - 4x2) (y2 + 4x2) = 2 (y4 - 16x4 )
Common factor of 2.
2 (y4 - 16x4 )
Differences of squares
2 (y2 - 4x2) (y2 + 4x2)
Difference of squares again.
2 (y-2x)(y+2x)(y+4x2) |
Equations:
Question 14:
Solve
2(x + 1) – 3(x – 1) = 20
(a) |
-15 |
(b) |
10 |
(c) |
21 |
(d) |
25 |
(a) |
-15 |
|
2x + 2 -3x + 3 = 20 => -x=15 => x = -15 |
Question 15:
Solve
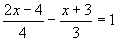
(a) |
1 |
(b) |
6 |
(c) |
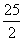 |
(d) |
18 |
(d) |
18 |
|
Multiply by 12 (3x4): 6x -12- (4x+12) = 12 => 6x – 12 -4x -12 = 12 => x=18
Multiply by 12 to eliminate fractions
3(2x-4)-4(x+3)=12
6x-12-4x-12=12
2x=36
x=18 |
Question 16:
Solve
2x2 – 5x = – 2
(a) |
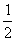 , 2 , 2 |
(b) |
-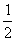 , -2 , -2 |
(c) |
-2, 3 |
(d) |
3, 2 |
(a) |
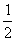 , 2 , 2 |
|
Use quadratic formula (put the equation in that form, ending with “=0”. )
D= b2 -4ac = (-5)2 -4 (2 x 2) = 9 >0, so we have two solutions.
Using the quadratic formula we get as solution x= 2 or x = 0.5
Checking tells us that both answers are correct.
2x2 – 5x + 2 =
0
Use quadratic formula with a = 2, b = -5, and c = 2
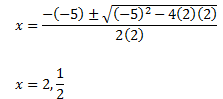
|
Question 17:
Solve
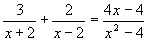
(a) |
No solution exists |
(b) |
-2 |
(c) |
2 |
(d) |
6 |
(a) |
No solution exists |
|
First simplify the equation (notice that (x+2) (x-2) = x2 -4, see exercise number 16!)
3(x-2) + 2(x+2) = 4x-4 => x=-2
Check solution
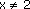
Cannot give a zero denominator, no solution exists. |
Question 18:
x2 – 2x – 5 = 0
(a) |
5, 3 |
(b) |
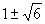 |
(c) |
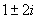 |
(d) |
no solution exists |
(b) |
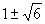 |
|
Use the quadratic formula. First calculate D= 24>0, so we have two possible solutions. The formula gives then gives us x = - 1.5 and x = 3.5. Only 3.5 (actually, 3.449) turns out to be a right answer. |
Question 19:
Solve
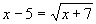
(a) |
9, 2 |
(b) |
9 |
(c) |
2 |
(d) |
6, 3 |
(b) |
9 |
|
Square both sides and put equation in form fitting the quadratic formula. D= 49, so we have two possible solutions. The formula tells us that x= 2 or x=9, however, if you check, 2 turns out to be an extraneous root.
Square both sides, let equation equal 0, and factor.
x=2 or 9
Check solutions
2 in an extraneous root
x=9 |
Question 20:
Solve
a4 – 13a2 + 36 = 0
(a) |
±3, ±2 |
(b) |
3, 4 |
(c) |
9, 4 |
(d) |
±3, ±4 |
(a) |
±3, ±2 |
|
First, this kind of equation will give us 4 possible solutions. To solve this, we need to start by stating x= a2. Now the equation is much easier! We find: (x-4) (x-9)=0, so a= -2, a= 2, a=-3 and a=3. All solutions work.
let a2=x x2-13x+36=0 (x-4)(x-9)=0 x=4, x=9
a2=4, a2=9 a=+2, -2, 3, -3 |
Question 21:
Solve
x – 9x1/2 + 14 = 0
(a) |
7, 2 |
(b) |
49, 4 |
(c) |
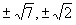 |
(d) |
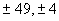 |
(b) |
49, 4 |
|
Take the 9x1/2 to the other side and square both sides of the equation, you get: (x + 14)2 = 81 x. You can solve this equation using the quadratic formula.
let x1/2=a a2-9a+14=0 (a-2)(a-7)=0 a=2, a=7
x1/2=2, x1/2=7 x=4, x=49 |
Question 22:
Solve
(x – 15)2 – 3(x – 15) – 18 = 0
(a) |
21, 12 |
(b) |
-9, -18 |
(c) |
6, -3 |
(d) |
15 |
(a) |
21, 12 |
|
First work out this equation to a more accessible form: x2 -33x+252=0. Now use the quadratic formula: D=81 ->two solutions. x= 12 or 21.
let a=(x-15) a2-3a-18=0 (a-6)(a+3)=0 a=6, a=-3
x-15=6, x-15=-3 x=21, x=12 |
Question 23:
Solve
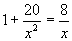
(a) |
5, 3 |
(b) |
2, 6 |
(c) |
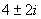 |
(d) |
There are no solutions |
(c) |
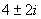 |
|
First bring all terms to one side, then multiply both sides by x2.
You get: x2-8x+20=0. D<0, so using the quadratic formula, find
the imaginary root of
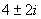 |
Question 24:
Solve
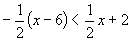
(a) |
x > 1 |
(b) |
x < 1 |
(c) |
x > -5 |
(d) |
x < - 5 |
(a) |
x > 1 |
|
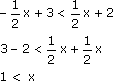 |
Question 25:
Solve
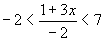
(a) |
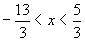 |
(b) |
1 < x < 5 |
(c) |
1 > x > - 5 |
(d) |
- 5< x < 1 |
(c) |
1 > x > - 5 |
|
Multiply all terms by -2, so the inequality changes: 4>1+3x>-14
Now take -1 off all terms (if this doesn’t seem logical, consider them as two separate equations): 3>3x>-15, which is 1>x>-5 |
![]()