Chemistry
Exercise 3
3. Understand the relationship between chemical bonding and physical properties.
The ideas of bonding, or how atoms stick together to form molecules, is sometimes confusing because there is more than one theory. The Lewis Theory (or octet rule) builds on our understanding of stable closed shell configurations to give a very simple but still powerful view. VSEPR (Valence Shell Electron Pair Repulsion) Theory expanded the Lewis idea to cover anomalies and hybridization was invoked to help explain how atomic orbitals might reconfigure to produce the shapes described by VSEPR. The most recent view of bonding is MO (or Molecular Orbital) Theory which combines atomic orbitals using an understanding of energy and symmetry to produce molecules, again it builds on the foundations of Lewis, VSEPR and hybridization. If we have a fundamental understanding of atomic structure and properties and bonding, it is not that difficult to predict many physical properties such as melting point, boiling point, solubility, lipophilicity, etc.
a) Use electro negativities to arrange the bonds listed in each part in the order of increasing ionic character.

http://chemistry.allinfoabout.com/features/electronegativity.html
Note: any introductory chemistry text will have a similar diagram or table with the electronegativity values listed for each element. The greater difference in electronegativity between two elements, the greater the ionic character of the bond between them.
i) O-F, I-F, In-F and N-F.
First determine the electronegativity value for each element:
O= 3.5, F = 4.0
In = 1.6, N = 3.0
I = 2.5
Now determine the electronegativity difference between each pair in the bond:
OF= 3.5-4.0 = 0.5 (take the absolute value of the difference).
IF = 2.5-4.0 = 1.5
InF = 1.6-4.0 = 2.4
NF = 3.0-4.0 = 1.0
Now just order them from smallest to largest
OF< NF <IF <InF
ii) O-H, O-F, N-H and N-F
First determine the electronegativity value for each element:
O= 3.5, F = 4.0
H = 2.1, N = 3.0
Now determine the electronegativity difference between each pair in the bond:
OF= 3.5-4.0 = 0.5 (take the absolute value of the difference).
OH = 3.5-2.1 = 1.4
NH = 3.0-2.1 = 0.9
NF = 3.0-4.0 = 1.0
Now just order them from smallest to largest
OF< NH <NF <OH
iii) N-S, N-O, N-Cl and S-Cl
First determine the electronegativity value for each element:
O= 3.5, Cl = 3.0
S = 2.5, N = 3.0
Now determine the electronegativity difference between each pair in the bond:
NS= 3.0-2.5 = 0.5 (take the absolute value of the difference).
NO = 3.0-3.5 = 0.5
NCl = 3.0-3.0 = 0
SCl = 2.5-3.0 = 0.5
Now just order them from smallest to largest
NCl< NS = SCl =NO
b) The following species are isoelectronic: CO, NO+, CN-, and N2.
i) Draw Lewis structures for each and include formal charges
Lewis structures can be constructed by following these strategies:
- Sum the total number of valence electrons for each atom in the molecule (this is based on the column of the periodic table in which the atom is found) to determine the total number of valence electrons in the molecule. For polyatomic anions, add one electron per negative charge and for polyatomic cations, subtract one electron per positive charge.
- Draw a preliminary framework for the molecule using single bonds. Keep in mind that the least electronegative atom is placed in the central position and hydrogen and halogens (F, Cl, Br and I) often occupy terminal (end) positions.
- Complete the octets of all atoms by adding lone electron pairs. Remember, hydrogen only requires two electrons to complete its octet
- Count all of the electrons (2 per lone pair and 2 per single bond). This number must equal the number of valence electrons counted in step 1. If the number of electrons is less than that in step 1, add electrons to the central atom. If the octet rule is not satisfied for the central atom and lone-pair electrons are nearby, use those electrons to make double or triple bonds to the central atom.
-
Check each atom to determine its formal charge; formal charge is calculated using the following formula
# valence e- in neutral atom - 1/2 (# bonded e-) – (# e- in lone pairs)
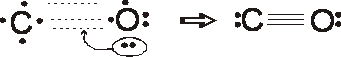
Formal charges
C = 4 – 1/2 (6) – 2 = – 1
O = 6 –1/2 (6) – 2 = + 1
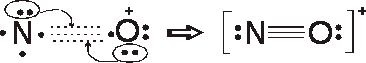
Formal charges
N = 5 – 1/2 (6) – 2 = 0
O = 6 –1/2 (6) – 2 = + 1
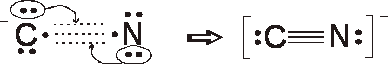
Formal charges
N = 5 – 1/2 (6) – 2 = 0
C = 4 –1/2 (6) – 2 = - 1
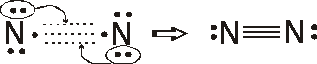
Formal charges
N = 5 – 1/2 (6) – 2 = 0
ii) Each of the four reacts with metal atoms or metal cations to form complexes. When a complex is prepared, we can assume that an electron pair from one of the four forms a covalent bond by occupying an empty orbital of the metal atom or metal cation. For each heteronuclear species, tell which atom is bonded to the metal.
AC in CO
C in CN-
N in NO+
c) Draw the resonance forms for the ozone molecule, O3, and for the sulphur dioxide molecule, SO2. The OO bond distance in O3 is 127 pm, which is between the OO single bond distance of 148 pm and the double bond distance of 110 pm. On the other hand, the SO bond distance in SO2 is 143 pm, which is shorter than either the SO single bond distance of 170 pm or the double bond distance of 148 pm. Explain.

S is located in the third period of the periodic table The SO2 bonds are shorter because they involve p and d Π electron interactions that shorten the bond, whereas oxygen does not have d electrons.
d) Find the wavelength (λ) in the indicated units for light of the following frequency:
i) 55 MHz (λ in m)
5.5 m
This problem can be solved using the following equation
![]()
where f is frequency in hertz, c is the speed of light in a vacuum (3 x 108 m/s) and λ is wavelength in meters.
![]()
![]()
e) Use the VSEPR theory to predict the geometric shape of the following molecules and ions. All the bonds in the structures are single bonds.
The VSEPR theory may be used to predict molecular shape based on bonding and non-bonding electrons around the central atom. The following table may be used as a guideline for determining molecular shapes based on the number of electron pairs.
| Bonded atoms | Non-bonding electron pairs | Bond angle | Molecular structure | Example |
| 2 | 0 | 180 | Linear | CO2 |
| 3 | 0 | 120 | Trigonal planar | SO3 |
| 2 | 3 | 120 | Angular | SO2 |
| 4 | 0 | 109 | Tetrahedral | CH4 |
| 3 | 1 | 107 | Trigonal pyramidal | NH3 |
| 2 | 2 | 104.5 | Angular | H2O |
| 5 | 0 | 120/90 | Trigonal bipyrimidal | PCl5 |
| 6 | 0 | 90 | Octahedral | PCl5 |
* these rows reflect total electron pairs. The molecular structure arising from these configurations will look to minimize the repulsion between non-bonding electron pairs by placing them as far apart as possible.
i) IF2+
Angular
Drawing out the Lewis structure shows the central atom (I) to be bonded to atoms and have 2 non bonding electron pairs (remember to subtract an electro fro the total number of valence electrons because it is a polyatomic cation). Hence, the shape is angular.

ii) IF2-
Linear
Elements beyond the second period are able to exceed the octet garden and thus can have more than eight electrons in their valence shell. Iodine exceeds the octet rule by using its 5d orbitals to accommodate extra electrons. IF2- has 22 valence electrons and after connecting the atoms I has 2 bonded atoms and 3 non-bonded electron pairs, hence the shape is linear.

iii) IF3
T-shaped
The IF3 molecule has 3 bonded electrons and 2 nonbonding pairs
around the central for a total of 5 areas of electron density. The two lone
pairs are in equitorial positions since. This is the preferred positions for
large lone pairs. Two of the bonding pairs are axial and the third is in the
equitorial plane. This leads to a T-shaped molecule.

iv) CIF4+
Irregular tetrahedron
ClF4+ has a total of 34 valence electrons. The molecule involves 4 bonded atoms and 1 non-bonding electron pair about the central Cl atom. Because there is a total of 5 areas of electron density, ClF4++ follows the configuration of IF3 above, with one non-bonding pair replaced by an atom. The resulting shape is an irregular tetrahedron; 3 fluorines bonded in a plane 120o apart, 1 fluorine atom bonded perpendicular to the plane and the electron pair above the plane.

v) CIF4-
Square planar
the ClF4- molecule has 36 valence electrons and an arrangement of 4 bonded atoms and 2 non-bended electron pairs around the central Cl. The overall configuration is an octahedral shape with the four F atoms bonded in a plane 90o apart and the 2 electron pairs occupying the space above and below the plane. This shape is referred to as a square planar arrangement

vi) CIF5
Square pyramidal
ClF5 follows a similar octahedral arrangement as the above ClF4-, the only difference being a replacement of one electron pair with a fluorine atom. The resulting shape is a square pyramidal, characterized by 4 atoms bonded in a plane, 90o apart and one atom bonded perpendicular to the plane at 120o.

f) Give an explanation for the following:
i) The dipole moment of OF2 is 0.30 D but the dipole moment of BeF2 is zero
BeF2 is linear; OF2 is not
Dipole moments arise out of an asymmetry in the electronegativity between atoms.
The dipole moments of the above molecules are related to the geometry of the molecules. Consideration of the Lewis structure shows that OF2 assumes an angular configuration (2 bonded atoms and 2 non-bonded electron pairs around the central oxygen atom). Beryllium is a 2nd period earth metal and does not obey the octet rule. Beryllium is electron deficient and its valence shell is satisfied with only two electrons. The resulting shape of BeF2 is linear because it contains 2 bonded atoms and zero non-bonded electron pairs about the central Be atom. Given these arrangements, OF2 has a net dipole while the electronegativity of fluorines in BeF2 are cancelled out due to the atom’s symmetry.

ii) The dipole moment of PF3 is 1.03 D but the dipole moment of BF3 is zero.
BF3 is trigonal planar; PF3 is not
Similar to Be in the above question, B may also exist in an electron deficient environment (ie it does not satisfy the octet rule). Thus, the molecular configuration of BF3 involves 3 bonded atoms and 0 lone electron pairs about the central B atom resulting in a symmetrical trigonal planar arrangement in which the electronegativity of the flourines is cancelled out by one another. PF3 on the other hand assumes a configuration of 3 bonded atoms and 1 lone electron pair and an overall trigonal pyramidal shape. The result is a net dipole directed from the phosphorous atom to the fluorines.
 |
 |
iii) The dipole moment of SF4 is 0.63 D but the dipole moment of SnF4 is zero
SnF4 is tetrahedral; SF4 is not
The shape of SF4 is generated by the arrangement of 4 bonded atoms and 1 non-bonding electron pair about the central atom, S, that is able to exceed an octet of valence electrons by utilizing its 3d orbitals. The overall shape is an assymetrical irregular tetrahedron, with 3 fluorines bonded in a plane 90o apart and 1 fluorine atom bonded perpendicular to the plane. The resulting dipole moment occurs between the sulphur and 4 fluorine atoms. SnF4, on the other hand assumes a symmetrical tetrahedral arrangement that has no dipole moment.
 |
 |
g) Explain why the following melting points fall in the order given
Increasing London forces
Melting points of compounds are largely influenced by intermolecular forces, with greater forces corresponding to greater attraction between molecules and thus higher melting points. All of the above molecules are symmetrical and therefore do not participate in dipole forces therefore the only intermolecular forces present are Van der Waals (London dispersion) forces. The magnitude of Van der Waals forces is correlated to the size of the atom, or more specifically, the number of electrons present. The above trends in melting points follows an increase in atomic number because greater electron density results in a greater polarizabilty of the molecules.
h) Calculate for the longest and shortest wavelength of visible light:
i) Wavelength in nanometers
shortest: 400 nm (violet)
longest: 700 nm (red) – this information can be obtained from a spectrum of electromagnetic radiation, found in any chemistry textbook
ii) Energy in Joules
Energy is calculated using the above wavelengths and the following formula:
![]()
where h is Plank’s constant (6.626 x10-34 J*s) and c is the speed of light (2.99 x108 m/s)
| Longest wavelength: | |
| Shortest wavelength: |